Heresy comes in different levels. For the modern intellectual, the lowest levels of heresy might be about politics or economics – areas of thought where you’re allowed to have unorthodox ideas without being excluded from polite company. Higher levels of heresy might be about religion or science – disagree with orthodox assumptions here, and you’ll be seen as quite-possibly-crazy. The highest level of heresy in the modern world is mathematical heresy. Disagreement with mathematical orthodoxy is synonymous with “being a full-blown crank.” You’re simply not allowed to doubt certain ideas in mathematics without being condemned as an intellectual leper.
Unfortunately, as with any other area of thought, there’s an inverse relationship between “acceptability of disagreement” and “likelihood of error.” The more taboo it is to challenge an assumption, the more likely it will collapse under scrutiny. Theologians might be able to tolerate disagreement about God’s properties, but they cannot tolerate disagreement about God’s existence. His existence is too foundational to revise. If God doesn’t exist, the entire theoretical structure built on top of this assumption gets destroyed.
So it is with mathematics. Several fundamental assumptions are not allowed to be challenged and have therefore turned into dogma, which makes this article mathematical heresy.
I’ve examined the foundations of standard Geometry and found two errors – one logical, the other metaphysical. This article will focus on the metaphysical. Essential objects described by mathematicians do not exist. Thus, any conclusions that are derived based on the existence of these objects are likely incorrect.
In this case, the universally-accepted claim that “Pi is an irrational, transcendental number whose magnitude cannot be expressed by finite decimal expansion” is false because of a metaphysical error.
Pi is a rational number with finite decimal expansion. This idea, that might seem inconceivable at first, will turn out to be overwhelmingly reasonable by the end of this article.
(For the rest of this article, I’ll abbreviate “Pi is a rational number with finite decimal expansion” as “Pi is a finite number” or more simply, “Pi is finite.”)
On Shapes
My claims are straightforward and preserve basic geometric intuition. For example, this is a “circle”:
This is a “line”:
And these are “points”:
If you believe these objects are indeed circles, lines, and points, then you too believe that pi is finite. You see, mathematicians do not believe these objects qualify as “lines” or “points.” In their minds, lines and points cannot be seen, and in fact, they’d say the above “lines and points” are mere imperfect approximations of lines and points.
To understand why, we have to ask a set of questions whose answers people assume have already been sorted out. These are questions that are supposedly so obvious that they aren’t worth asking. And yet, when we ask them of mathematicians, we get dubious answers. Questions like:
What is a “shape”?
What is a “line”?
What is a “point”?
What is a “circle”?
What is “distance”?
Ask your average intellectual these questions, and they’ll likely scoff at you, because they assume, “Everybody knows what a line is!” They are wrong. I, for one, do not think that mathematicians know what lines are. And because their theories are built on their metaphysical claims about “lines and points,” the theories must be revised from the ground up.
Without Length, Breadth, or Sense
As pi is the subject of this article, let’s lay out the definition that we’ve all learned in school:
Pi is the ratio of a circle’s circumference to its diameter.
We’ve got a few key terms in here: “the ratio”, “a circle”, “circumference” and “diameter”.
In order to understand what pi is, we need to understand what these other terms mean. Especially this one: “a circle.” Here’s one definition:
A “circle” is a shape whose boundary consists of points equidistant from a fixed point.
Sounds reasonable. A few more key terms we need to understand: “shape”, “boundary”, and “points.” If we want to understand pi, we must understand what circles are, and if we want to understand what circles are, we must first understand what “points” are.
It’s here that I find the fundamental error plaguing orthodox geometry: the definition of a point, from which all other geometric objects are constructed. What is a point? Turns out, there are many different definitions. We’ll start with Euclid’s original definition, which I like.
A “point” is that which has no part.
We’ll come back to that definition later. Here’s another one:
A “point” is a precise location or place on a plane.
Not bad. They are often represented by little dots:
However, these intuitive definitions aren’t actually workable in modern mathematics. “Points”, in orthodox geometry, aren’t really “defined” per se. They are supposed to be understood in terms of their properties. An essential property is this:
Points do not have any length, area, volume, or any other dimensional attribute. They are “zero-dimensional” objects.
This is absolutely foundational to modern conceptions of geometry. Points cannot have any length, width, or depth to them. And yet, all shapes are supposedly constructed out of them. So you might ask, “Hang on, how can shapes, which have dimensions, be composed of a bunch of points that do not have dimensions?”
That’s a very good question, and if you insist on finding a logical answer, you will end up like me: rejecting very large parts of orthodox mathematics.
Every “line”, to a mathematician, is actually composed of an infinite number of points – yet, each point is itself without any dimension. Lines, which have length, are composed of points, which have no length. How does this make sense?
It doesn’t.
It’s like asking, “How many 0’s do you have to add together to get a 1?” The answer is obvious: you can’t add a bunch of 0’s together and get a 1 – not even an infinite amount of 0’s. If a point has zero dimensions, then it doesn’t matter how many you put together. You’ll never end up with a dimensional object. This is a logical necessity.
So, we have a very big problem. The literal foundation on which the entire theoretical structure of modern geometry is built – the “point” – is dubious. Errors at this level could be catastrophic.
Shapes Without Shape
If consistent, the mathematician quickly forces himself into odd positions. For example, he must conclude things like, “We cannot see shapes!” Take the example of what non-mathematicians call a “line”:
Certainly, this cannot be a line to a mathematician, because lines supposedly have only one-dimension – length. This object has both length and width – it is extended in two dimensions. What can we call this shape, then, if not a “line”? I don’t know – you’ll have to ask a mathematician.
What about a two-dimensional object: the circle?
Certainly, this cannot be a circle. This object is composed of pixels, not points, and each pixel is itself extended in two dimensions. Therefore, the object has rough edges and isn’t perfectly smooth. Though laymen might call it a “circle,” it’s only a mere approximation of the mathematical circle, sometimes called the “perfect circle.”
The same can be said for the mysterious “point”:
These objects cannot qualify as “points” either, because they have dimensions. We can see them, after all. Mathematical objects cannot be seen; they cannot be visualized; they cannot have any extended – or “actual” – shape. If an object actually has shape, if it takes up space, then it’s got to be made up of spatially-extended objects akin to computer pixels, not mathematical points.
Note: I’m not just talking about “physical space” or “physical shape”. I’m talking about shapes of any kind. What I see in my visual field – blobs of color – have shape, but they are not physical objects. They themselves do not occupy physical space. They are mental representations, and they are made up of extended points of light – pixels on my mental screen.
So, a natural question arises:
Has anybody, ever, seen or experienced these mathematical shapes in any way? Has anybody encountered even one true “line” or “circle”? The answer must be an emphatic “No.” All of the “lines” and “circles” that we actually experience have dimensions. They are constructed from a finite number of points which themselves have dimensions. The objects we experience are composed of pixels.
The importance of this point cannot be overstated.
This means every “circle” you’ve ever seen – or any engineer has ever put down on paper – actually has a rational ratio of its circumference to its diameter. Every “circle” that’s ever been encountered has a unique “pi” that can be expressed as ratio of two integers.
“Circumference”, for any circle we can experience, can be understood as “the shape’s outermost boundary”, which is itself composed of a finite number of pixels. It’s “diameter”, too, is a simple integer – the number of pixels which compose it. Put one integer as a numerator and one integer as a denominator, and you’ve got a rational pi.
In fact, these truths should be uncontroversial, even for mathematicians:
Every “circle” you’ve ever encountered, without exception, has a rational, finite pi.
No “circle” you’ve ever encountered, without exception, has an irrational pi.
So, that means my claims about a “rational pi” are true for at least 99.9999% of all shapes that we call “circles”. It also means that pi is unique to any given circle. This shouldn’t come as a surprise, however, when you think about the nature of ratios.
Imagine I were to say, “What is the ratio of a table’s height to length?”
You would naturally respond, “Which table?”
The same is true of circles. There is no “one true ratio called ‘pi’” for the same reason there is no “one true ratio of a table’s height to length.” Each table, and circle, is constructed by a finite number of units, arranged in different ways, and therefore their ratios will vary.
According to standard geometry, there is literally only one “circle” that my claims don’t hold true for: the so-called “Perfect Circle” – an object so mysterious that no mortal has ever encountered it.
The Divine Shape
This “perfect circle” does not have any measurable sides or edges. Its boundary is composed of an infinite number of zero-dimensional points. The outermost points take up exactly zero space. Its pi cannot be expressed by any decimal expansion – nor will we ever know exactly what its pi is.
This object cannot be constructed, visualized, or even exist in our world. Our world is too imperfect for it. Instead, it lives in another realm that our minds can faintly access.
The Perfect Circle is so great, that all other “circles” are mere approximations of it. It is the one true circle. If you ask for proof of its existence, you will find none. Yet, the mathematicians have built their entire geometric theory based upon its existence.
I freely admit my heresy: I do not believe in the “perfect circle.”
Therefore, I do not believe in the “irrational pi.” Nor do I have any need for such a concept. Every shape I’ve ever encountered – or will ever encounter – has edges that take up space.
A geometry without perfect circles, and without the irrational pi, is fully sufficient to explain all of the phenomena I experience. Therefore, I’ve no need to posit an extra entity – especially one with such remarkable properties.
In other words: I simply believe in one less circle than mathematicians. That’s all that’s required to conclude that pi is a rational number for any given circle.
Just an Abstraction!
I’ve heard some mathematicians claim that geometric objects are mere abstractions and are therefore exempt from the preceding criticism. But among other things, this gets the metaphysics of abstraction backwards. You abstract from concretes. You don’t concrete from abstract.
Think about it. From what does one abstract in order to get the concept of a “perfect circle”?
It cannot be the circles we actually see, since every one of those circles has imperfect edges. All of the concrete experiences we have are of shapes with imperfect edges, a rational pi, and are made up of points with dimension. So from these experiences, the mathematician says, “Well, I think that a true circle is one without edges, with an irrational pi, and is made up of zero-dimensional points!”
This is nonsense, and it’s not the way abstraction works.
Imagine we’re talking about houses and abstract conceptions of houses.
Every house we’ve ever encountered has walls, a floor, and a ceiling. The mathematician wants to say that his conception of a “perfect house” is one without walls, floors, or a ceiling. And in fact, regular ol’ houses are mere approximations of his perfect house. Obviously, this is a mistake.
We can have a perfectly valid abstract conception of a house, but the properties of our “abstract house” must include the properties of the concrete houses we’re abstracting from. Our “mental house” has to include the conceptual categories of “having walls, floors, and a ceiling.” The dimensions of these properties are irrelevant, so long as they are existent.
An abstract conception of “a house without walls, floors, or a ceiling” cannot explain any phenomena we experience, because it describes no thing that could possibly exist. Imagine your friend takes you to an empty field and says, “Here’s my perfect house! It’s got no walls, floors, or a ceiling!” You’d think he was crazy – especially if he added, “And all other houses are a mere approximation of it!”
Not Real!
One of the more self-incriminating responses from mathematicians goes like this, “But mathematical objects are not real! They don’t exist at all!” In all my research, I can confidently say that mathematics is the only area of thought where admitting “the objects I’m talking about aren’t real and don’t exist” is meant to defend a particular theory.
This error is a conflation of objects and their referents. For example, the concept of “my house” is supposed to refer to “my house in the world.” It would be silly to say “My house doesn’t take up space, because my idea of my house doesn’t take up space.”
Similarly, the conception of a “point” is supposed to refer to “a precise location in geometric space.” It would be equally silly to say “points don’t take up geometric space, because my idea of a point doesn’t take up geometric space.”
The fundamental essence of geometry is about space – whether physical space, mental space, conceptual space, or any other kind of space. Therefore, the objects of geometry must themselves take up space. There is no such thing as “a precise location in space that isn’t a precise location in space.”
An Alternative Theory
So, let me present an alternative geometric framework. This is just the beginning of a whole new theory of mathematics that I call “base-unit mathematics.” This is the fundamentals of base-unit geometry:
1) All geometric structures are composed of base-units. These units are referred to as “points.”
2) Each point is spatially extended.
3) In any conceptual framework, the extension of the base-unit is exactly 1. Within that framework, there is no smaller unit of distance, by definition.
4) All distances and shapes can be denominated in terms of the base-unit.
These foundations form a logically sound foundation on which to build geometry.
Put points together, and you can compose any shape you like, without any irrational numbers. Every object except the base-unit is a composite object, made up of discrete points. This is why I said earlier that I like Euclid’s original definition of a “point” as “that which has no part.” Base-units have no parts; they are the parts which form every other whole.
I recognize there will be lots of objection to this way of thinking about geometry. Those objections will be addressed in detail in future articles.
To gain an intuition about this framework, you can think of “points” as “pixels”, which we all have experience of. All of the shapes and objects you might encounter in a hi-res VR simulation are actually clumps of pixels, though they might appear “perfectly smooth” from our macroscopic perspective.
A few of the nice implications of this theory:
This is a line:
This is a circle:
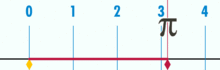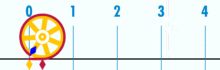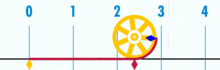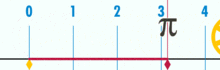
And it has a demonstrably rational pi:
(Note: this GIF was taken from Wikipedia to show the supposed irrationality of pi. Yet, if you’re aware of what you’re watching, it’s actually a demonstration of the rationality of pi. You’re looking at a GIF of the logical perfection and precision of base-unit geometry!)
What’s the ratio of this circle’s circumference to diameter? Simple: it’s one integer over another – however many base-units make up the circumference, divided by however many units make up the diameter. And, as it so happens, as long as the circle isn’t constructed from a tiny amount of base-units, pi ratios will work out to around 3.14159 (Though, if we’re being perfectly precise, we must denominate in terms of fractions, as decimal expansion can be dubious within a base-unit framework. But that’s a future article.). There is no “generic” or “ideal” circle. There are concrete, actual circles, each of which is a composite object constructed by a finite number of points.
Among other things, this also means there’s no such thing as a “unit circle” – a supposed circle with a radius of 1. There are no diameters that have a distance of 1. You can’t create a circle using only one pixel.
Within this theory, “circles” are exactly what you’ve encountered. “Points” are locations in space that are actual locations in space, and “lines” are what everybody knows they are.
Base-unit Intuition
Obviously, this topic requires a lot more explanation and work, not just in geometry, but everywhere that the metaphysics of mathematics is mistaken. I cannot cover all the objections to base-unit geometry in this article, but I will explain a few more ways of thinking about it and why it’s superior to standard orthodoxy.
First of all, this framework fully explains all of the phenomena we experience, and it loses exactly zero explanatory power when compared to standard Geometry. Every shape, every circle, every line, every point, every spatial experience that we’ll ever have can be explained, without positing the existence of extra entities. We do not experience perfect circles; therefore we’ve no reason to theorize about them.
Furthermore, base-unit math is more logically precise than the orthodoxy. Anybody who’s worked with “irrational pi” must use approximations. They cannot use an actual infinite decimal expansion. They are forced to arbitrarily cut off the magnitude for pi in order to use it. Not so with base-unit geometry. Perfect precision is actually possible, since there are no approximations or infinite decimal expansions to deal with. This might not be a big deal right now, but as technology approaches the base-unit dimensions of physical space, it might actually make a big difference.
Here’s a short, interesting aside about pi’s infinite decimal expansion:
What’s going on when orthodox mathematicians are calculating out further and further decimals of pi? Are they grasping at “the Perfect Circle’s true ratios”? No. What they’re doing is calculating the pi ratios for circles with ever-smaller base units. As the base unit shrinks – or as the circle gets larger in diameter – the ratio of its circumference to diameter changes ever-so-slightly. These calculations are immediately practical, in the same way that trig tables are practical. They are pre-calculated values that are applicable and accurate for a given circle of a given size.
(If you want to understand why pi changes slightly, think of it this way: as the size of the base-unit increases, the area enclosed by the circumference shrinks; as the size of the base-unit decreases, the area enclosed by the circumference increases, yet at a diminishing rate. The smoother the edge of the circle, the larger the area of the circle.)
On this note: base-unit geometry does not require an “ultimate base-unit.” In other words, every conceptual scheme will have a base-unit by logical necessity, but that doesn’t mean you’re prevented from coming up with a different conceptual scheme that has a smaller base unit.
Think of it this way: any given photograph will contain a finite number of pixels. It will have a base-unit resolution. However, that doesn’t mean it’s impossible to take a photo with higher res. Similarly, any given circle will have a base-unit resolution, but that doesn’t mean it’s impossible to conceive of one with higher res (smaller base-units).
We might even run into the limits of the physical world. Physical space must have a base-unit, which means within our physical system, there is no smaller unit. However, that doesn’t mean we’re prevented from talking about smaller-dimensional base units. Those objects simply won’t correlate to our universe. Who knows – perhaps we could say true things about a different physical universe that has smaller base-units.
Note: this also perfectly correlates with my resolution to Zeno’s paradoxes. Space must have a base-unit, if motion is possible.
A great example of base-unit phenomena is the fractal. Supposedly, fractals only make sense within the conceptual framework of “infinite divisibility.” This is not correct. Fractals make much more sense within a base-unit context. Consider this image:
This looks like a prime candidate for “infinite divisibility.” However, it’s an illusion. At any given time, there is a base-unit resolution to this image. As the image “zooms in”, new units are created, all denominated in terms of pixels. At no point are you looking into infinity; you’re always looking at a finite number of pixels. If you doubt this, you may count the pixels. The object is being constructed as you watch it. The same happens in mathematics; the objects get constructed as you conceive of them. Much more will be said about this in future articles.
Polygons and Greeks
I want to quickly address one objection that will inevitably arise – those who claim that the images of circles in this article aren’t actually circles; they are polygons. The edges are a bunch of little straight lines; they aren’t perfectly smooth. If this is true, then it’s no criticism of base-unit geometry, because all the round objects that we encounter would be polygons. Therefore, our mathematical theories should be about polygons; we experience nothing else. I want to know about the properties of this shape:
I don’t care what you call it. Base-unit geometry can tell you about the properties of that shape.
The Greeks also made this mistake when talking about circles – as if they were constructed from an “infinite number of lines.” This is incorrect. Circles and polygons are composed of a finite number of points, not lines. Lines don’t compose anything; they are themselves composite objects.
Imagine constructing a circle in the sand.
What is the area of this circle? I guarantee it’s a finite, rational number. You can literally count the grains of sand which compose it. The circumference is composed of grains of sand, as is the diameter, as is the area. They are all integers.
The last argument I will address in the article will come from those who think a “circle” isn’t a shape; it’s a mathematical expression. Something like (x² + y² = r²).
This is just another metaphysical confusion that conflates symbols with the object the symbols are supposed to be describing. It’s like saying, “’Apples’ are synonymous with the words ‘a red fruit.’” This is confused. The words “a red fruit” are a description of the object, not the object itself. The formula like (x² + y² = r²) will describe the shape of a circle – or, if you prefer thinking about it this way – it’s a rule for constructing a circle. It is not itself a circle.
That’s where I’ll end this article. There is much more to say in the future. Mathematics is not exempt from criticism or skeptical inquiry. Nor is it exempt from the need for precise metaphysics. For all the reasons I outlined in this post, there is plenty of room for alternative – and superior – conceptions of geometry. Base-unit geometry loses no explanatory power, eliminates an infinite number of unnecessary objects, and gives a logical foundation on which to build a stronger theory.
If you don’t believe in the existence of “perfect circles” – made up of an infinite number of zero-dimensional points – then you do not believe pi is irrational, and you’ve joined an extremely small group of intellectual lepers. You may now expect mockery and condemnation for your heresy.
If you enjoyed this article and would like to support the creation of more heresy, visit patreon.com/stevepatterson.