Humans are lazy when thinking about infinity. Usually it doesn’t matter, but sometimes, our imprecision comes with big philosophical implications. Profound logical errors permeate mathematics – in calculus and set theory in particular – due to an inaccurate conception of infinity.
The definition of “infinite” or “infinity” has slightly different meanings depending on the context, but the core concept is the same: without inherent limit. Contrary to the colloquial use of the term, infinity is not a really big number. It’s not even a really, really big number. It’s a concept that means “never ending”. Never fully encapsulated. Non-completeable. Or literally, “non-finite”.
There’s a logical category difference between the finite and the non-finite. They can never be mixed. You cannot contain infinity within the finite – if it’s contained, it’s necessarily non-infinite. This might sound obvious, but because of the implications, it’s worth rephrasing several ways. All of the following are logically necessary propositions:
An infinite series of tasks cannot be finished. (If the series is finished, it’s finite)
An infinite distance cannot be fully covered. (If the distance fully covered, it’s finite)
A finite amount of space cannot contain an infinite amount of space. (If space is contained, it’s finite)
A finite amount of matter cannot contain an infinite amount of matter. (If matter is contained, it’s finite)
An infinite series can never end. (If the series ends, it’s finite)
These are all true by definition. Yet, this goes against many standard mathematical principles – approaching an infinite limit, the convergence of infinite series, and the existence of infinite sets. Physicists speculate about infinite densities, infinite masses, and infinite forces. The same error plagues them all: a logical category mistake. “Infinite” and “finite” are not treated as mutually exclusive, which they are by definition.
Convergence of Infinite Series
Take the convergence of an infinite series – a central idea in Zeno’s paradoxes. Supposedly, an infinite series can “converge” into a finite sum. But mathematicians play loose with the definition of “convergence”. In a strict sense, “to converge” means “to get arbitrarily close to— but not actually reach — a finite sum.” Yet, when applied to concrete situations, mathematicians and philosophers use it to mean “to get arbitrarily close to — and then actually reach — a finite sum.”
For example, let’s say John is trying to sprint eight yards. He’s at location 0, and his goal is location 8. Before he reaches 8, he has to go through the mid-way point: location 4. Then, he has to cross the next mid-way point, between 4 and 8: location 6. Then again, half way between 6 and 8 is location 7. Then 7.5. Then 7.75. Then 7.875. Then 7.9375, ad infinitum. No matter how close he gets, there will always be a half-way point he has to cross.
Zeno concluded: therefore, since an infinite number of points can never be crossed, motion is impossible. Most modern philosophers disagree. They say, “Calculus solves that! Motion is possible because the infinite series converges onto the final location.” They argue, “As John gets closer to the final point, the amount of time required to transverse the distance also shrinks. The distance gets halved, but the time required to travel that distance also gets halved! Therefore, at some point, these two series terminate on location 8.”
Indeed, the standard resolution to Zeno’s paradoxes proclaims calculus is the answer. But both Zeno and modern mathematicians (and philosophers) are wrong. Zeno’s logic was sound, but his conclusion was unnecessary. Mathematicians’ logic is contradictory, therefore their conclusions are false.
The solution is simple: it is impossible to complete an infinite series, but physical reality is not infinitely divisible. To the extent that motion is possible, it must be the case that space-time has an indivisible base-unit. (Make sure to read this post for more explanation.)
This is not a hypothesis, nor is it a question to be resolved by mathematical calculation. Simply examining our concepts reveals a certain truth: if a series is infinite, it is certainly not finite, and therefore, it can never fully converge. To the extent that a series fully converges, it is certainly non-infinite.
To put it as clearly as possible: a non-terminating series can never terminate. This is a logical necessity.
Unfortunately, mathematics is riddled with denials of this truth. They say things like, “Take a whole pie and divide it in half. Then, divide it again, and again, and again. You can keep dividing, ad infinitum, and you’ll still be left with a whole pie. Therefore, this shows that infinity can be contained within the finite.”
A clear logical contradiction. The concept of infinite divisibility does not apply in the real world. You cannot contain what cannot be contained. If you can contain it, it certainly isn’t infinite. You cannot “add up an infinite amount” of real pie-particles and get a finite pie. Regardless of how small the pie-units are, if you have an infinite amount of them, then you have an infinite amount. Therefore, you do not have a finite amount of pie.
“One” does not equal “infinity-added-together”.
Point Y Shows the Problem
Here’s another way to think about it:
Take our runner, John. He started at point X. He’s reached his final goal at point Z. When he was at point X, he certainly wasn’t at point Z. When he arrived at point Z, he certainly wasn’t at point X. That means, at some point, he made that final leap to point Z.
Examine the very first instant he arrived at point Z. Now, back up one instant – just before he arrived. That instant must exist, and it must be after point X and before point Z. Call it “point Y” – the penultimate point.
Point Y’s very existence is logically incompatible with an infinite series.
After all, we’re saying, “point Y is the very last point before Z”. But infinite series cannot have “a very last point”. If a series has a very last point, it is finite by definition.
If you respond, “then there is no point Y”, that’s the same as saying, “there is no point just before reaching point Z”. In other words, you’ve doomed the runner to never arrive at Z. If he can’t cross Y, he certainly cannot reach Z.
The resolution is clear: if motion is possible, then point Y exists, and it must be the case that there isn’t an infinite amount of points between X and Z. In other words, there must be a base-unit of distance.
To ask, “Well how long is half of one base-unit?” is merely a mental exercise, not correlated to anything in physical reality.
The Leftover Principle
One more way to understand the problem: the leftover principle. Let’s take our pie example again (where one whole pie represents any finite quantity of X). Imagine we try to construct the pie by adding a series of halves together. Each addition is half the previous one. So we start with half a pie. Then we add a fourth. Then an eighth. Then a sixteenth. Let’s say that we continue this infinitely. We always add half the previous amount – never two identical halves together (which would complete the whole). Would we ever end up with a whole pie?
No. Absolutely not. You will always have some emptiness left over – another way of saying the pie will never be whole. The series of half-slices will never fully converge into a whole pie. We can know this with certainty by examining our concepts.
Take any amount and divide it by two. What does that mean? It means you’ve divided something in half. Anything divided in half has two parts. Always. If we only take one part, we are always going to have another part leftover. This is a logical necessity. “Taking one half” implies “leaving one half.”
Splitting something in two leaves you with two amounts. That’s what we mean by “splitting something in half” or “dividing by two”. If you only take one amount, you’ve left one amount. If you split the remaining amount in two, and only take one half, then you must still have leftovers.
If this process doesn’t change, it doesn’t matter how long you continue it. An infinitely long process of taking halves will never end up with a whole.
In fact, if you’ve ended up with a whole, it must be because the process of taking halves terminated.
So, if we see a whole pie in front of us, we can know it isn’t comprised of an infinite series of decreasing amounts. It isn’t infinitely divisible. One question illustrates: at some point, has the very last bit of pie been added to make a whole? If yes, then we’re not dealing with an infinite series (as “the very last bit” is incompatible with infinity). If no – the very last bit of pie has not been added – then we’re not dealing with a whole pie.
This is true of any finite amount of anything – distance, time, particles, etc. Going “half the distance towards Z” always means “leaving distance remaining”.
You cannot keep leaving distance remaining, infinitely, and wind up not leaving distance remaining.
But Calculus Works!
Mathematicians or physicists might respond, “That’s a bunch of Greek philosophizing. Calculus just works. We can make extremely precise predictions incorporating infinities into our calculations, so it obviously isn’t a logical error.”
This response does not give enough weight to logical reasoning. It doesn’t matter if somebody claims they can “demonstrate” a logical contradiction, and it doesn’t matter if that demonstration is useful. If it involves logical contradictions, it’s wrong. Logic trumps mathematics, physics, and every other discipline. Zeno had that part right.
Fortunately, I can preserve all the beauty and predictive power of calculus with the same resolution presented above. Calculus works because there’s a fundamental unit of spacetime. At some point, the calculations get down to the smallest base-unit, where reality precisely conforms to the equations.
It is impossible to “approach an infinite limit” – infinity is by definition something which cannot be approached. We can’t get closer to it. But we can approach (and fully arrive at) a really, really small or really, really big number. The calculations work the same. We’ve no reason to interject infinity into anything.
Looking at Infinity
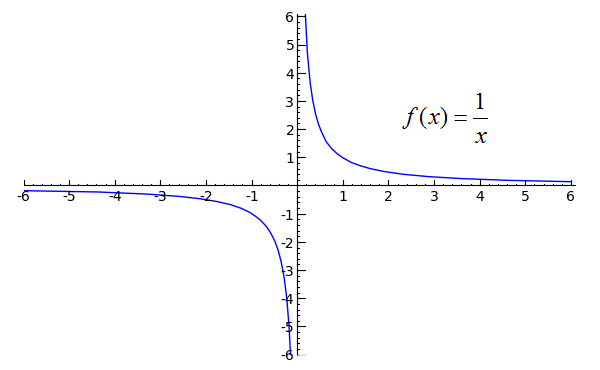
Using a loose definition for infinity just adds to the confusion surrounding the concept. For example, take a simple graph of a function:
In standard mathematical lingo, we’d say the X and Y axes are “asymptotes” of the curves, meaning the distance between the line and the curve approaches zero as they tend towards infinity. But if we want to remain committed to a precise use of the term “infinity”, we need to be extremely careful.
First, a sensible interpretation of the graph: as X grows larger, f(X) shrinks. There is no inherent limitation of values you can use for X.
Now, an irrational interpretation: in actuality, these curves are infinitely long, and this graph is showing just a small snapshot of them. Infinity exists ”out there”, and we are looking at a tiny section of it.
This mistake is the ubiquitous Platonic error in mathematics. (Read more about mathematical Platonism here.)
To avoid nonsensical ideas, we musn’t be confused about the metaphysical nature of mathematics and numbers. Numbers are concepts – they aren’t ethereal, independent “entities” separate from our conception of them. So when you look at a graph, you aren’t peeping at Platonic “lines” which exist in the ether. The line doesn’t exist until you create it, and it doesn’t exist in places it’s not been created.
Instead, you’re looking at a visual representation of the logical relationship between numbers – between the exact numbers you’ve used in your equation. Each time you plug numbers into your equations, you will have concrete values, and nothing more. The above graph ends at 6-and-a-hair. The lines do not stretch beyond it.
You might think to yourself, “There is no limit to the value of the numbers I can plug into this equation, and I know the curves will not meet the asymptotes.” And this is true for logical reasons. But it is quite different from thinking, “These lines have a real existence that stretches infinitely into a Platonic realm, never meeting their metaphysical asymptotes.”
(Note: the traditional “calculus solves it!” response to Zeno’s paradox claims that, at some point, the curve actually reaches the asymptote – a logical impossibility.)
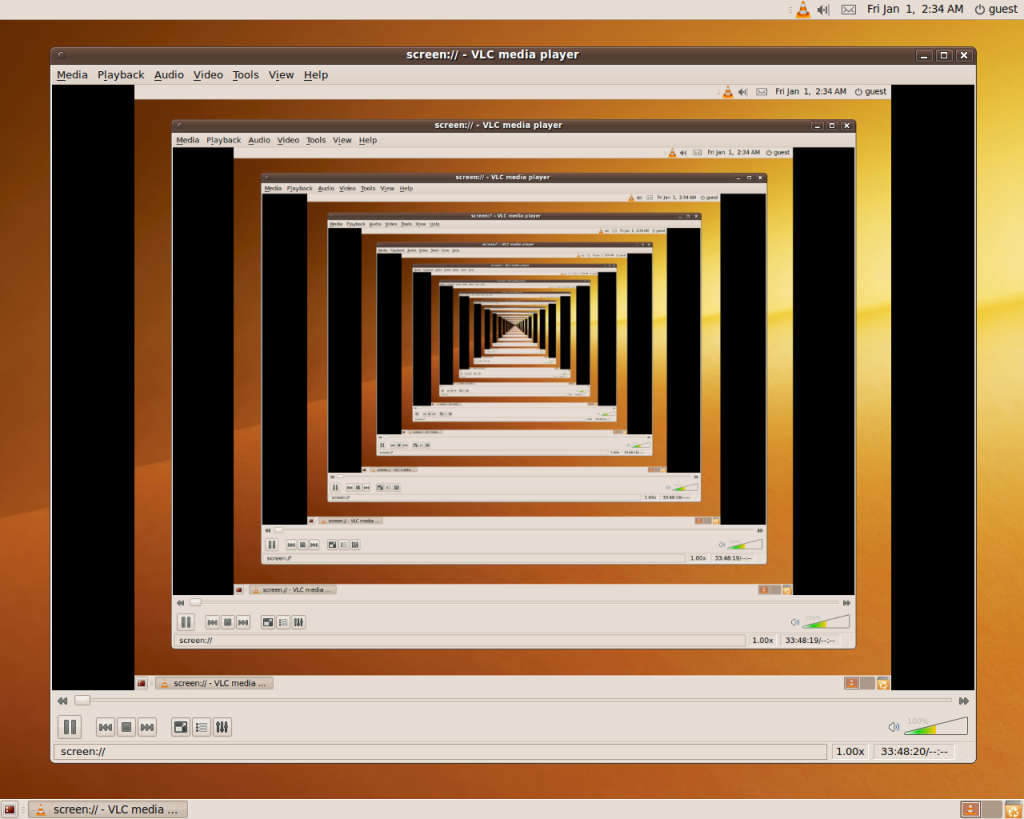
You cannot graph infinity, by definition, nor can you have infinite lines, but you can create a graph which sparks the concept of infinity in your mind. You can conceptualize plugging in larger numbers, but the graph in your mind will be finite. You cannot concretely imagine an “actualized infinity”. But, you can certainly write special symbols which convey the concept of “unending”. This picture does the job:
What are we looking at? Infinity? No, of course not. We might have the idea sparked in our minds, but we’re looking at a picture with a finite amount of pixels – 838,656 to be exact. Not one pixel more. It terminates in reality. Take the biggest computer screen in the entire world – make it the size of our solar system. It will eventually terminate.
If you continue the recursion process past what’s represented here, that’s something you’re adding additionally. Though of course, you cannot concretely imagine this pattern being repeated an infinite number of times. Every picture in your head will be finite.
To avoid confusion, we musn’t interject infinities into places it doesn’t exist.
A Clearer Conception
Whenever we want to use the term “infinite”, we must understand it as a concept. A statement about limitations. A never-ending process. It isn’t an adjective to describe concrete objects. There is no “infinitely large number” in reality – that concept doesn’t even make sense. If it’s a number, it isn’t never-ending. A clearer phrase would be, “We cannot imagine a number so large that we cannot add one to it.” That’s the only sensible way to rescue the phrase, “an infinite amount of numbers exist.”
We must also eliminate logically contradictory ideas like “an infinite circle” or “an infinitely long line”. There are no such things, any more than there exists “a square circle”. If a circle is a circle, it is a finite circle by definition. If it’s a concrete circle, then it isn’t an infinite circle. If we want to remain sensible, we can say, “There is no inherent limit to the size of circle I can imagine.” But of course, that doesn’t mean “All sizes of circles exist in the Platonic realm.” The same is true of lines, shapes, or any other object, whether conceptual or physical. You can create finite geometric shapes of any magnitude in your mind.
Or, how about this standard textbook phrase: “a line is made of up of an infinite number of points”. This is no more sensible than saying, “a finite sum is made up of an infinite number of sums.” If a point represents anything concrete, then there certainly isn’t an infinite amount of them in a finite line – it doesn’t matter how small the “points” is. If you respond, “Well, a point doesn’t take up any space”, then your point is merely a conceptual tool and does not reference anything concrete. And you will not find a concept embedded in a line. It is a logical necessity: you cannot have a finite line composed of an infinite number of actual, spatially-represented points.
The same is true of distances, forces, densities, and magnitudes. There is no actual distance between two points which you can say, “Aha! Now that’s an infinite distance!” If it’s an actual distance between two points, it is not a never-ending distance.
This is true for an even deeper topic: the existence of “infinite sets” – a foundational idea in modern mathematics. For reasons I’ve laid out in this article, the idea of an “infinite set” is logically contradictory and metaphysically nonsensical, but I will devote an entire separate article to set theory; the implications are enormous.
What about basic division? How many times is 10 divided by 3? Simple: three times, and you have one remaining. You cannot perfectly divide 10 by 3. You can represent this truth in decimal form – 3.3333… – and you might get close, but it will never be perfectly accurate. The same is true of pi. What is it? Well, you can try to represent it in decimal form, and you can get close, but it will never be perfect. So, we give it its own symbol. It’s a mistake to expect everything to be perfectly representable in decimal form; it’s just a language like any other.
All of these conclusions follow from simple premises: what is infinite is not finite. What does not end, does not end. What cannot be encapsulated, cannot be encapsulated. What does not fully converge, does not fully converge. What has no boundaries, has no boundaries. What cannot be completed is never completed.
These are logical truths, not speculative hypotheses. No amount of calculation will prove otherwise.
(Update: I recently came across this video, which accidentally demonstrates the extreme absurdities that result from infinity errors.)