Paradoxes don’t exist. But they can teach us something about our ideas. Whenever we discover a contradiction in our beliefs, we’re forced to make revisions. Paradoxes can help us elicit nestled contradictions in our worldview that we wouldn’t see otherwise.
Some of the most famous and oldest paradoxes in the world are Zeno’s paradoxes. He came up with several, but I just want to focus on the most famous one.
And defend it.
Usually, paradoxes need to be carefully resolved – they bury subtle logical errors within them. But with Zeno, the logic is sound. What isn’t sound is his conclusion. He thought he proved that motion is impossible. But instead, he proved something unique about physical reality.
I think his arguments are brilliant, and they revolve around the difficulties that “infinity” presents us with. Modern philosophy usually overcomes Zeno by saying “Calculus solves the problem!” But this is mistaken. Logic actually solves the problem, not mathematics. I will write extensively in the future about some problems I see in mathematics – specifically the presupposition of Platonism, and the treatment of infinities (in set theory, in particular).
Before I explain the paradox, I want to commend Zeno on his commitment to philosophical rigor; we must follow logical argumentation wherever it leads, as he did, regardless of how unintuitive the conclusions appear. We do not gain insight into the world by believing what appears to be true – rather, what necessarily follows from what, with logic as the final judge.
Zeno’s Paradox
So the paradox goes like this. Let’s take two examples. In the first, consider a train traveling to its destination. It has to travel 100 feet. Before it completes its journey, it must first pass the half-way point: the 50 foot mark. Then, it must travel through the next half-way point, leaving 25 feet remaining. Then again, it must go through the half-way point, leaving 12.5 feet remaining. Then again, and again, and so on, down to just inches. Then half-inches. Then half-half-inches. This can continue ad infinitum. There’s no possible distance which can’t be divided in half, and the train must pass through each point. Because it’s impossible to fully complete an infinite set of tasks, the train will never arrive.
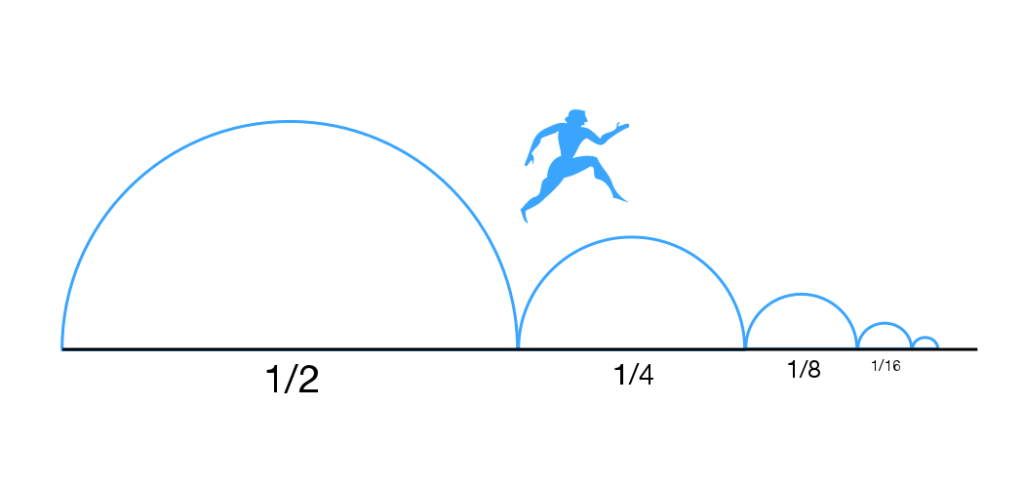
Work through the logic of this argument, broken down into four parts:
a) It is necessarily impossible to complete an infinite set of tasks.
b) At every point along the path, there always remains a “half-way mark” which must be crossed.
c) An infinite amount of half-way marks cannot be crossed.
d) Therefore, the path can never be fully completed.
If A and B are true, then C and D necessarily follow. Zeno concluded, “And therefore, motion is impossible.” He went farther, outright rejecting all divisions between things and claiming that the most logical position is mysticism – that “all is one”.
One more example, then I’ll present my alternative resolution to the paradox. Consider a race between Fred and Mary, where Mary has a small head start, but Fred is much faster. Zeno argued that Fred can never win the race, because he’ll never be able to catch up to Mary, and it’s a matter of pure logic.
In order for Fred to overtake Mary, he must first pass the point which Mary started from. Then, in the time it took for Fred to do this, Mary has moved a little bit forward. Fred must again make up that new distance. But when he arrives, Mary has again moved forward in that time.
Each time Fred arrives at Mary’s previous point, time has elapsed, which mean Mary has covered new distance. Because there’s an infinite number of points which Fred much reach where Mary has already been, he can never overtake her.
Again, work through the logical power of this argument:
a) Before Fred can overtake Mary, he must cross every point she has crossed.
b) In order for Fred to reach Mary’s previous point, time must elapse.
c) Every time time elapses, Mary creates new distance.
d) Fred must cross that new distance, which also takes a certain amount of time, creating new distance to cross.
e) No distance can be crossed without time elapsing.
f) Therefore, Fred will never be able to get ahead of Mary.
These are profound arguments. Concluding that “Motion must be impossible” is not as ridiculous as it first sounds. The modern response is usually, “But calculus solves it!” without much more offered. Sure enough, calculus gives us incredible precision in predicting events like Fred passing Mary. It conforms to our daily experiences – we witness motion all the time and don’t treat skepticism towards it seriously.
But mathematical calculations do not have the final say in matters of logic.
An infinite series of events cannot be completed, by logical necessity of what we mean by “infinite”. It doesn’t matter how well the calculations work. So where does that leave us?
Fortunately, I have a resolution which preserves logical necessity, calculus, and a clear definition of “infinite”.
The Answer
It’s simple: Physical reality is not infinitely divisible. There is a base unit.
Revisit the train example. As the train is nearing its destination, it has to travel over the half inch point, half-half inch point, half-half-half inch point, etc. But this doesn’t continue infinitely, if there is a base unit. When there are two base units to go, it still has to go half way and travel over one of them. And then there’s only one unit left. Since there’s no meaningful “half-base unit” – at least not represented in physical reality – the train can arrive at the station without having to cross any more half-way points.
This means that “dividing a base unit in half” is merely a mental exercise, not possible in physical reality. In fact, this must be true, by virtue of what we mean by “base unit”.
So, when looking at the four part breakdown of the train argument, the mistake is with premise B:
“At every point along the path, there always remains a ‘half-way mark’ which must be crossed.”
This is not true. At some point, you are one indivisible unit away from your destination. Therefore, conclusions C and D do not follow, and we eject infinity from the argument.

Now, let’s revisit the race between Fred and Mary. It, too, gets resolved by a base unit in physical reality. The infinity is harder to see, but it’s buried in premise C:
“Every time time elapses, Mary creates new distance.”
This presupposes that time and space are infinitely divisible. If we reject that idea, then we can see there’s some amount of time in which Mary would not move even one base unit. If this is true, that’s all which is required for Fred to pass Mary, assuming he’s moving faster than she is.
You could think of it this way: instead of their speeds being calculated in MPH, imagine they were in IBUPS – indivisible base units per second. Fred might move a trillion IBUPS, while Mary only a hundred billion. Then, it becomes clear to see that Fred will overtake Mary in X seconds, depending on how far away he is.
The idea of a base unit is not exclusive to philosophy. In Physics, these are called “Planck units”. There’s Planck time, Planck length, etc. And to the extent that motion is possible, I’d say that their existence is necessary for the reasons Zeno pointed out. (though, it’s possible the details are different than the physicists think)
In this view, calculus is also preserved, while avoiding infinities altogether. In a future post, I will write more fully about infinites, but the base-unit-explanation allows us to purge them completely from our calculations. If we think of the train needing to cross “infinite series of points” in order to arrive at its destination, we’ve already doomed it to never arrive. With a base unit, we needn’t deal with the “infinitesimal distances” (what I see as a contradiction in terms), infinite limits, or anything of the sort. Instead, we are left with concrete, smallest-required numbers for our calculations. There’s only so many decimal places you need to go in order to be perfectly precise.
The Pixel Theory
I’ll offer one more theory which can explain motion while preserving Zeno’s logic. I call it the “pixel theory” of physical reality. It requires we tweak our idea of motion slightly. Imagine the physical world is made up like your computer screen –a fixed structure containing a zillion little spaces for tiny “pixels”.
When you see your cursor move across the computer screen, you’re not actually seeing “motion” as we think about it – you’re seeing a progression of little dots firing in succession. Like one of those LED signs. When you see letters move across the sign, you’re just seeing bulbs firing in a particular pattern. There’s no letters moving at all.
Motion could simply be the firing of little physical pixels in succession, based on particular inputs in the world. In fact, this is precisely what happens when you watch a movie on TV. You see what appears to be regular motion in the physical world – people moving around and such – but it’s not that at all. It’s just a motionless screen giving the illusion of movement.
You might say: motion is the transmission of energy across the “screen” of physical reality. The pixels just pop in and out of existence; they don’t move anywhere.
This explanation also preserves logical sense, avoids infinities, and Zeno himself might like the conclusion. Either scenario is logically possible, but they both require the same thing: a base unit of physical reality, either fixed or in motion. This should not be controversial, however, when you think about it.
Infinity and Logic
Imagine an empty container. Does an infinite amount of space reside within it? Of course not. But if it were true that physical reality were infinitely divisible, it would mean that infinity resides within the finite! It doesn’t matter how little the particles are – if there’s an infinite amount, there’s a non-finite amount of space occupied by them.
Take two points A and B, and draw a line between them. Are you looking at an infinitely long line? Of course not. You’re looking at two finite points being joined by a finite line.
If you respond, “But points do not take up space”, then I respond “Then your ‘point’ is a concept, not something within the line.” You cannot meaningfully reference a “point” which does not take up space. If it doesn’t take up space, then it has no spatial existence and cannot be used as a unit of length.
All of these conclusions flow from simple premises. You cannot progress over an infinite distance in a finite time. You cannot add up infinity to get a finite number. You cannot contain infinite space within finite space. You cannot complete an infinite series of events – an infinite series is necessarily non-completeable. I will write another post on infinities, but Zeno understood their logical power. From my perspective, though he got his conclusion wrong, his reasoning was sharp, and he inadvertently proved that, to the extent motion is possible, we necessarily live in a finite world. Logic requires it.