Countless thinkers for the past two thousand years have appealed to Euclidean geometry as an example of rock-solid reasoning. The proofs in Euclid’s Elements are beautiful deductive structures. One proof builds on the next, and by accepting the starting axioms, you are compelled to agree with the final conclusions.
The geometric objects within Euclid have properties which can be grasped by logical reasoning alone—e.g. the reason we don’t believe that parallel lines touch is because of understanding the concept of parallel lines, not by observing and measuring them in the world. Kant famously considered this an example of synthetic a priori reasoning and wondered how it could be possible.
Moderns have since rejected the idea of the geometric a priori, thanks to the discovery of non-Euclidean geometries in the 19th century. And thanks to Einstein in the 20th, physicists claim that our own universe is non-Euclidean—space is curved by mass, they say. That’s what gravity is all about.
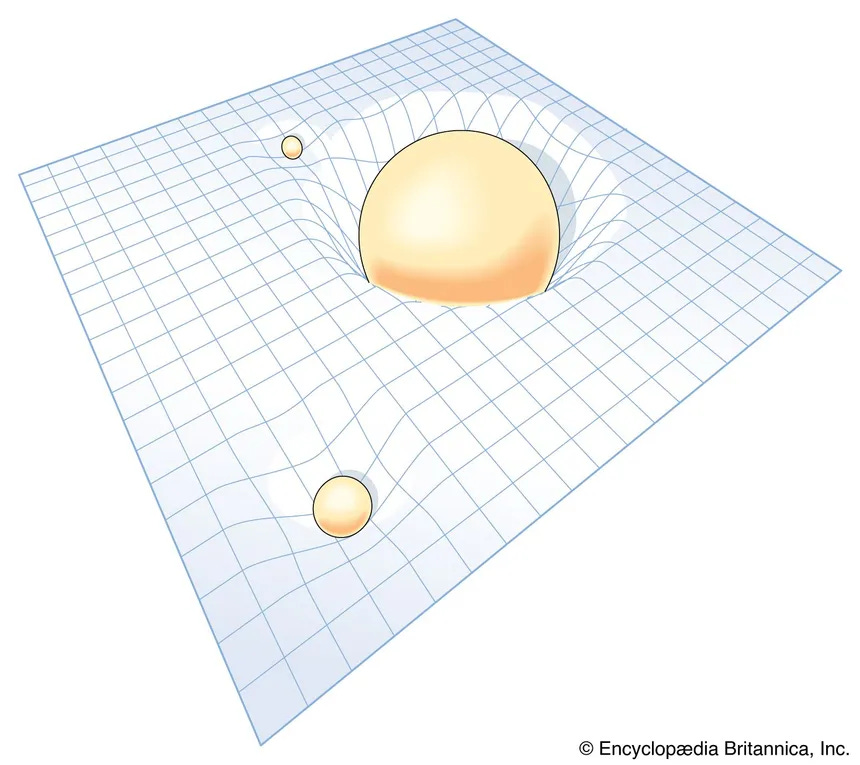
Geometry Meet Economics
When I was researching the fundamentals of Austrian Economics and their distinctive methodology, there were often analogies drawn to Euclidean geometry—i.e. the unshakeable axioms of human action in economics are akin to the unshakeable axioms of Euclid in geometry. You don’t go out and measure whether the interior angles of a triangle add up to 180 degrees! You just know it by understanding what ‘triangle’ means!
When I first heard these analogies, I rather liked them. All of my geometric intuitions were Euclidean, and I hadn’t heard about non-Euclidean geometries before.
As I learned more, I discovered the history of non-Euclidean geometries. I’d speak with Austrian-types about it, but they tended to be skeptical and would ask questions like: What does it really mean for space to be curved?
Clever mathematicians and physicists say odd things like, “You see, straight lines can sometimes be circular! It just requires space to be curved!” And my skeptical Austrian friends would roll their eyes. Physicists are just playing word games; straight lines cannot be curved by definition!
I like this criticism. Since that time, I’ve spent a lot more time thinking about these topics and have become critical of the extreme apriorists in economics. And I don’t believe the axiomatic appeal to Euclid works. But not for the reason you might think.
No Curved Space—>No Curves At All
The problem is not with the notion of a priori geometry. From what I can tell, mathematicians and physicists are playing word game when talking about “curved space.” I don’t think that concept makes sense. It’s useful for building practical models, but that doesn’t make it true or even coherent.
The problem isn’t just with the traditional non-Euclidean notion of “curved space.”
The problem is with the Euclidean conception of curves.
Ultimately, curved space doesn’t make sense for the same reason that curved lines don’t make sense: curves don’t make sense at all!
The reason is actually quite simple: the traditional understanding of curves presupposes the infinite divisibility of space. Euclid, along with 99.9% of everyone else, presupposes that space is a continuum—that between any two points of space, there are an infinite number of additional points. Infinities within infinities.
If you reject the notion of infinite totalities and do not believe space is a continuum, then that means curves don’t exist. Or at least, it means that the curves that obviously do exist work different than we’ve been told.
I would like to hereby resurrect the notion of the geometric a priori and claim, by appealing to pure conceptual analysis, that geometry does have an underlying logical framework that we all presuppose in order to make sense of things. That framework is non-Euclidean, not because space is curved, but because space is actually discrete.
Therefore, the traditional conceptions of “points” and “lines” and “spheres” will have to be reformulated accordingly. If you don’t yet have the finitist intuition, examine the following image of “curved space” closely enough until you see its underlying discreteness and total lack of smooth curves.
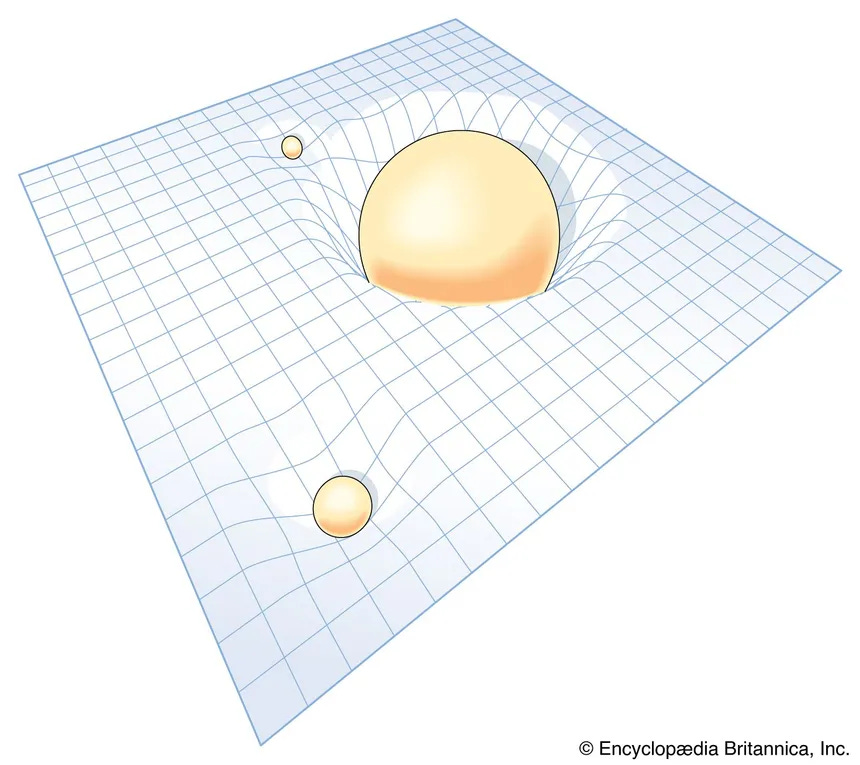
(If necessary, move your physical eye closer to the screen until you see the pixels.)